LRFTubes example: a Helmholtz resonator¶
© 2018 - ASCEE
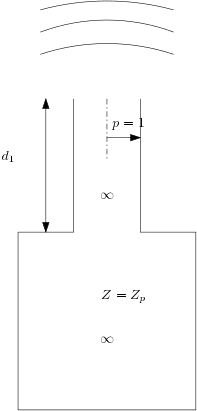
This example describes the procedure to find the resonance frequencies of a Helmholtz resonator. A Helmholtz resonator is a type of compact acoustic resonator. A typical examples of a Helmholtz resonator is a beer bottle. The figure below shows the Helmholtz resonator we are going to model:
In [1]:
# Import necessary stuff
%pylab inline
from lrftubes import Air, System, Volume, PrsDuct
Parameters¶
Firstly, the parameters are defined:
In [2]:
# Temperature
T0 = 300. # Kelvin
p0 = 1e5 # Pascal
# Initialize the material
air = Air(T0=T0,p0=p0)
Lneck = 2e-2 # 2 cm
rneck = 1.5e-2/2 # 1.5 cm
Sneck = np.pi*rneck**2
# Volume of the compliance volume
Vvol = 0.3/1000 # Say, about 0.3 litres
# Dissipating area of the compliance volume, assuming the volume is a cube
Svol = Vvol**(1/3)**2
Construct the system¶
Next, we construct the system and we connect the nodes
In [3]:
# Create a 'neck' prismatic duct
neck = PrsDuct(cs='circ',S=Sneck, L=Lneck)
# Create a volume, where inertial effects are neglected
vol = Volume(Vvol,Svol)
# Create a system, add the segments and boundary conditions
sys = System(air)
sys.addSeg(0,1, neck)
sys.addSeg(1,2, vol)
# Set volume flow on right node equal to zero
sys.addBc('U',2,0)
# Set pressure at entrance equal to unit Pa
sys.addBc('p',0,1+0j)
# Create a array of frequencies to solve for
freq = np.linspace(100,1000,500)
# Solve the system for all frequencies
sol = sys.solve(freq)
In [4]:
# Benefit from the easy dictionary indexing of the solution as a function of the frequency
# Absolute value of the velocity amplitude.
absu_top = np.abs( sol[neck]['UL']/Sneck )
# Plot the velocity amplitude vs the frequency.
figure(figsize=(12,6))
plot(freq,absu_top)
xlabel('Frequency [Hz]')
ylabel('$|u|$ [m/s]')
_=title('Amplitude of the velocity response at the neck outlet of the Helmholtz resonator')
In [5]:
# Maximum
print("Resonance frequency according to the model:", end='')
res_freq_model = freq[np.argmax(absu_top)]
print(' %0.2f Hz' %res_freq_model)
print("Resonance frequency according to lumped theory:", end='')
res_freq_lumped = air.c0/(2*np.pi)*np.sqrt(Sneck/(Vvol*Lneck))
print(' %0.2f Hz' %res_freq_lumped)