LRFTubes example: side resonator insertion loss¶
© 2018 - ASCEE
This example shows the computation of the insertion loss by adding a side resonator to a pipe. The situation is as follows:
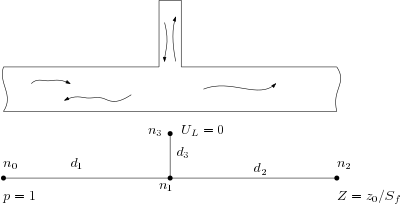
The impedance at the rightmost side is equal to $z_0 / S$, such that no reflections come back from that side. This way, the insertion loss can be computed by the ratio of the acoustic pressure on the right side by the incoming wave on the left side. As we would expect, the insertion loss peaks at the quarter wave resonance frequency of the side pipe.
In [1]:
# Import necessary stuff
%pylab inline
#%pylab
from lrftubes import Air, System, PrsDuct
In [2]:
# Define the geometry
r = 0.15
r1 = r # Radius of duct 1
r2 = r # Radius of duct 2
r3 = 0.4*r # Smaller radius for the side resonator
S1 = np.pi*r1**2
S2 = np.pi*r2**2
S3 = np.pi*r3**2
L1 = 1.
L2 = 1.
L3 = 0.6
d1 = PrsDuct(L=L1,S=S1,cs='circ')
d2 = PrsDuct(L=L2,S=S2,cs='circ')
d3 = PrsDuct(L=L3,S=S3,cs='circ')
mat = Air()
# Create the system, add the segments and boundary conditions below
sys = System(mat)
sys.addSeg(0,1,d1) # Duct 1 gets nodes 0 and 1. Node 1 is the branch node of the side resonator
sys.addSeg(1,2,d2) # Duct 2 connects to node 1 and has free node 2
sys.addSeg(3,1,d3) # Duct 3 is connected with its right side to the branch
sys.addBc('p',0,1)
sys.addBc('U',3,0)
z0 = mat.z0 # Characteristic impedance (lossless), rayls
sys.addBc('Z',2,z0/S2) # Set a characteristic impedance on the acoustic volume flow at node 3
freq = np.linspace(10,1000,500) # Create frequency array
sol = sys.solve(freq) # Solve the system
In [3]:
# Compute the incoming wave at the left side
figure(figsize=(12,6))
A = 0.5*(sol[d1]['pL'] + z0*sol[d1]['UL']/S1)
abspR_ov_A = np.abs(sol[d2]['pR']/A)
IL = -20*np.log10(abspR_ov_A)
semilogx(freq, IL)
title('Insertion loss of the side resonator as a function of the frequency',size=18)
xlabel('Frequency [Hz]')
_=ylabel('IL [dB]')
In [4]:
# Comparison with
print("First resonance frequency insertion loss according to the model:", end='')
quarter_wave_freq_model = freq[np.argmax(-abspR_ov_A)]
print(' %0.2f Hz' %quarter_wave_freq_model)
print("First resonance frequency insertion loss according to first principles:", end='')
quarter_wave_freq_fp = mat.c0/L3/4
print(' %0.2f Hz' %quarter_wave_freq_fp)